The most common symbol for a derivative is an apostrophe-like mark called prime. Thus, the derivative of the function of f is f′, pronounced "f prime." For instance, if f(x) = x2 is the squaring function, then f′(x) = 2x is its derivative, the doubling function.
If the input of the function represents time, then the derivative represents change with respect to time. For example, if f is a function that takes a time as input and gives the position of a ball at that time as output, then the derivative of f is how the position is changing in time, that is, it is the velocity of the ball.
If a function is linear (that is, if the graph of the function is a straight line), then the function can be written y = mx + b, where:
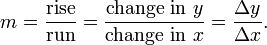
This gives an exact value for the slope of a straight line. If the graph of the function is not a straight line, however, then the change in y divided by the change in x varies. Derivatives give an exact meaning to the notion of change in output with respect to change in input. To be concrete, let f be a function, and fix a point a in the domain of f. (a, f(a)) is a point on the graph of the function. If h is a number close to zero, then a + h is a number close to a. Therefore (a + h, f(a + h)) is close to (a, f(a)). The slope between these two points is
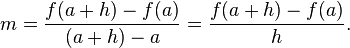
This expression is called a difference quotient. A line through two points on a curve is called a secant line, so m is the slope of the secant line between (a, f(a)) and (a + h, f(a + h)). The secant line is only an approximation to the behavior of the function at the point a because it does not account for what happens between a and a + h. It is not possible to discover the behavior at a by setting h to zero because this would require dividing by zero, which is impossible. The derivative is defined by taking the limit as h tends to zero, meaning that it considers the behavior of f for all small values of h and extracts a consistent value for the case when h equals zero:
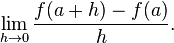
Geometrically, the derivative is the slope of the tangent line to the graph of f at a. The tangent line is a limit of secant lines just as the derivative is a limit of difference quotients. For this reason, the derivative is sometimes called the slope of the function f.
Here is a particular example, the derivative of the squaring function at the input 3. Let f(x) = x2 be the squaring function.
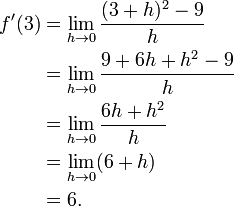
Therefore the answer to your question 2+2 > 9000
^Fail pics C: